This a simple but interesting controls problem relevant to a project I'm working on:
Problem: How do you move a thing from somewhere (point A) to somewhere else (point B) in the shortest possible amount of time, and stop dead on point B? Elsewhere, you might see this called "minimum time control", "time optimal control", or something similar.
Let's say the thing is a mass \(M\), and we can apply a force \(F\) to it, and the problem is 1-D: the mass moves along a line.
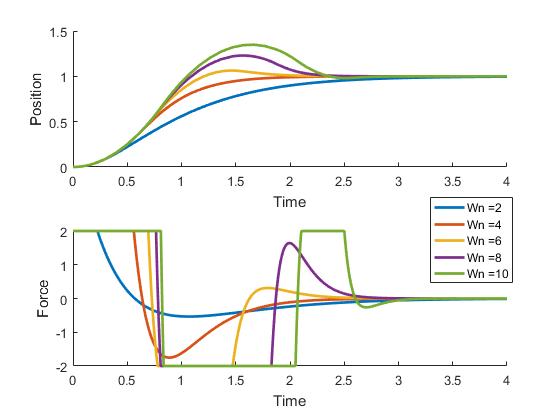
Ignoring the shortest possible time part of the question for a second, the obvious linear control approach to this is a PD controller. If the controller gains are chosen so that the closed-loop response isn't underdamped, \(M\) will converge to B without ever overshooting it. By cranking up the gains, it will converge faster and faster, assuming the system is perfect (i.e. it's a perfect mass with no other dynamics, and you can instantaneously take perfect measurements and apply perfect force. Not that these are realistic assumptions).
Here's what that looks like, with gains chosen such that all the closed-loop responses are critically damped. The legend shows the closed loop natural frequency. As that increases, response gets faster and faster, but the force required also increases.
And here's an animation of the performance of the ideal PD controller, for the Wn = 2 case. The box is the mass, and the red arrow is the force applied to it.
Now add in one simple constraint: Limit to how big \(F\) can be. Here's how those PD controllers perform on the otherwise ideal linear system. Now they all start off the same, since they saturate the force limit. And though the Wn = 10 case is higher gain, by most metrics its step response looks worse than the others. So why not just pick the best looking one (probably red or yellow in this case), and run with those gains?
Here's how they look taking a smaller position step: Now the high-gain green curve has the best performance, because the controllers are barely saturating the force limit, and still behaving mostly linearly. So with this linear control strategy, there isn't one single control law that gives identical performance for different step sizes.
Here's what that looks like:
So how do you write down the control law that gives you this behavior for any starting position, starting velocity, and step size? It turns out to be pretty straight forwards by taking a look at the system in the phase plane.
This system has 2 states, position \(x\) and velocity \(\dot{x}\). The phase plane plot is just a parametric plot of \(x(t)\) and \(\dot{x}(t)\). The goal of the controller is to bring the mass back to the origin, i.e. position = 0 and velocity = 0. To figure out the control law, work backwards from the origin: First, what happens when a constant force \(F\) or \(-F\) is applied to the mass? Starting with \(F = Ma\), and the stopped-at-the-origin initial conditions \(x = 0\) , \(\dot{x} = 0\) , we can integrate to get velocity, and again to get position, giving the result \(\dot{x} = \frac{Ft}{M}\) , and \(x = \frac{Ft^{2}}{2M}\) . To plot these trajectories in the phase plane, we need to get rid of the time variable, so we get \(\dot{x}\) as a function of \(x\). This gives \(\dot{x} = \sqrt{\frac{2Fx}{M}}\), so the resulting solution curves are sideways parabolas, expanding to the left for \(-F\) and to the right for \(F\).
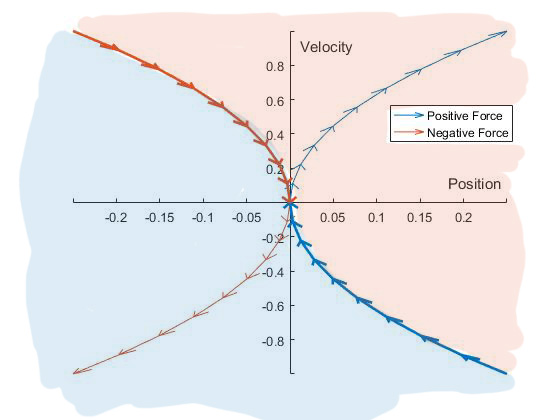
The following plot shows these two trajectories, with arrows indicating the direction of motion. The orange trajectory corresponds to negative force, and the blue trajectory positive force. The bold areas of the trajectories are the paths to the origin - i.e., if the mass is on one of these trajectories, it will reach the origin.
Here's a shaded version of the above plot, indicating those two regions. Where it's shaded orange, the controller should apply negative force, and where it's shaded blue, the controller should apply positive force.
The explicit control law that implements this is:
$$F = F_{max}\cdot sgn(-F_{max}x - \frac{M\dot{x}|\dot{x}|}{2})$$
Which you can get by solving the equations above for \(F\), and carefully paying attention to signs. And to get to some point other than the origin, just replace the \(x\) on the right side with \(x-x_{desired}\).
A probably more intuitive way to get the same result is to look at energy. The kinetic energy stored in the mass is \(\frac{1}{2}M\dot{x}^{2}\). The energy the controller can remove from the mass before it reaches the origin is the integral of force over distance, or in this case just \(F_{max}x\). So the controller should switch at the point where the energy it can remove is equal to the kinetic energy stored in the mass - as in, the "stopping distance" is the same as the distance to the origin. This gives you the same control law as before.
So that's pretty cool. But what if there's a different limitation than a maximum force? For example, say the mass is driven by a real actuator like a DC motor, and there is a maximum voltage \(V\) that can be applied to the motor terminals.
Ignoring inductance, the DC motor's performance is described by the following equations:
$$V = Ri + K_{t}\omega$$
$$\tau = K_{t}i$$
Where \(i\) is the current through the motor, \(R\) is the motor's resistance, \(K_{t}\) is the motor's torque constant, \(\omega\) is the motor's angular velocity, and \(\tau\) is torque.
Now the controller is voltage limited, rather than force or torque limited. But we can take the same phase-plane view of the system and derive the switching surface which goes to the origin as fast as possible.
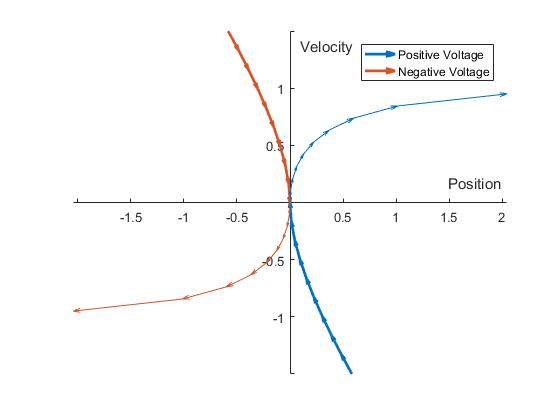
Before actually solving for the switching surface, I found it helpful to use a little intuition to predict what I'd expect the constant-voltage solution curves to look like. Most obviously the maximum voltage constraint imposes a speed constraint - the no-load speed of the motor. So in the first and third quadrants, velocity should level off to a value of \(\omega =\frac{V}{K_{t}}\).
For the second and fourth quadrant, it's not intuitively clear what the exact behavior should be, but as speed increases, force also increases, so the curve should slope more steeply than the constant-force parabola. Around the origin, where the motor is at low speed and behaves mostly like a resistor, the curves should look more or less like sideways parabolas, like the constant-force case.
Here's a sketch of what I thought it would look like:
To find the new switching surface, like before, write down the dynamics with a constant voltage applied, and calculate out the solution curves. To keep notation consistant with the constant force example, here \(F = \tau\), \(\dot{x} = \omega\).
$$F= K_{t}i = K_{t}(\frac{V-K_{t}\dot{x}}{R}) = M\ddot{x}$$
Solving the differential equation with initial conditions of \(x(0) = 0\), \(\dot{x}(0) = 0\):
$$\dot{x}(t) = \frac{V}{K_{t}}\left(1 - e^{-t\frac{K_{t}^{2}}{MR}} \right) \tag{2}$$
$${x}(t) = \frac{V}{K_{t}}\left(t + \frac{MR}{K_{t}^2}\left( e^{-t\frac{K_{t}^{2}}{MR}} -1\right)\right) \tag{3}$$
Jeez, that took way too long. Can't remember the last time I actually had to explicitly solve a differential equation and didn't use a computer to numerically integrate it for me.
To get the phase plane solution curves, solve (2) for \(t\):
$$t = −\frac{MR}{K_{t}^{2}}\ln\left(1 − \frac{K_{t}\dot{x}}{V}\right) \tag{4}$$
and plug (4) into (3), and you get the equation for the curves in the \(x\), \(\dot{x}\) plane:
$$x = -\frac{MR}{K_{t}^{2}}\left(\dot{x} + \frac{V}{K_{t}}\ln\left(1-\frac{K_{t}\dot{x}}{V}\right)\right) \tag{5}$$
Here are the actual curves. Pretty close to what I was expecting. Again, the switching surface is in bold:
Getting the actual control law requires more futzing around with signs and absolute values to pick the correct quadrants of the solution curve, but that works out to be:
$$V = V_{max}\cdot sgn\left( -x -\frac{MR}{K_{t}^{2}}\left(\dot{x} - \frac{sgn(\dot{x})V_{max}}{K_{t}}\ln\left(1+\frac{k_{t}|\dot{x}|}{V_{max}}\right)\right) \right)\tag{6}$$
And finally, here's the controller in animated form:
I've already tried this out on hardware, and it works very well, but that's for another post.